Real Time In-situ Thickness and Refractive Index Determination when Monitoring Multi-atomic Monolayers .
.
F. FERRIEU1 and C.VALLEE2 .
1Optical Polarimetry Ellipsometry. CH-6945 (Switzerland).
2 SUNY POLY, CNSE, ALBANY (USA).
Abstract: In situ Spectroscopic Ellipsometers (SE), is a precious real time process control tool. As frequently reported in literature, very thin layers measurements don’t yield however simultaneous and uncorrelated values for the thickness tF and the material refractive index (ri). Thickness values are highly related with the choice of an a priori assumed ri which a characteristic of the intrinsic layer’s nature. The paper implements an earlier analysis of the initial Drude equations. We show that when thickness turns ultra-thin then the ellipsometry equations can be solved through a first order expansion in tF. During growth, deposition or in the case of physical adsorption on a substrate, this hypothesis is entirely fulfilled. After describing the simple way to process data, within Atomic Layer Deposition (ALD) examples, it is shown how few physisorbed monolayers case can be handled so far. More general molecular physisorption is also considered. Particularly in the CO2/H2O gas adsorption inter exchange, ellipsometry turns a right method with absorbent like thin or native sub-oxide samples. Both refractive index and thickness with high accuracy are independently reachable and within a rather fast acquisition capability. In vacuum chambers, the stability of alignment is just being done one time and fully optimized. A fixed physical configuration inside vacuum chambers acts with benefit over usual limiting factors. An evident interest appears in atomic layer deposition or etching as well for molecular beam epitaxy and chemical vapor depositions techniques, and sputtering. With today’s “no moving part” or “one single shot” photonic technologies, Spectroscopic Ellipsometers within this configuration can provide sensitivity more than Surface Plasmon Resonance SPR which measures only the optical thickness. With the use of a limited number of wavelengths, SE exist in wide applications fields and furthermore depolarization factor acquisition gives an additional information on the player building accomplishment. Since the pioneer works from H. Arwin, a large opening for bio photonic sensors appears also today. Thin silica interacting with ambient is recognized as specific adsorbents material for gases and proteins detection which is observed here in “native” oxides layers.
1 Introduction
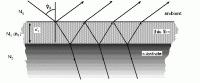
While easily detected, mono-layers as well as thin layer below few nanometers, are not so easy to analyze with Spectroscopic Ellipsometry (SE). Many examples exist as well from various fields especially in biology with adsorbed mono layers. Initially described as “transition layer” by P. Drude [1], this “top” monolayer can be assimilated also to a physisorption, porosimetry phenomena and/or atomic layers deposited or grown by molecular beam epitaxy processing. However even when considering a wide spectroscopic range or and with variable angle techniques, it was finally admitted that SE does not really solve this goal. For monolayers the main issue is how to determine simultaneously two parameters. As for porosimetry, in biology applications,[2-3], H. Arwin quoted earlier : ”it is often stated that it is impossible, or at least very hard, to resolve both tF and nF for a thin film in an ellipsometry experiment”. Today, new photonic designs are implemented in SE instruments. The technique has been presented as a potential tool in parallel fields like immunology testing of the “Adsorption of Proteins at Solid Surfaces” [3-6] This is something which turned as a crucial expectation in today’s researches in immunology as an antigens body detection tool.
Indeed different methods like surface plasmon resonance (SPR), measure optical thickness and as well refractive index variation [5][6] and an intensive efforts is given today to increase their precision . In fact the refractive index is expected to be known at almost within a 10-3 to 10-4 accuracy limits. Does ellipsometry could be used as well ?. In fact some developments based on the very early Drude descriptions[1], lead research today to reconsider the Fresnel equations as well. In other terms, this approach should turn into an unambiguous determination of both refractive nFilm and film thickness tfilm in this few nanometers range .Since several years, in a last publication has given a promising answer[7] . Though a review and the analysis of the theory is at first mandatory here.
Below 5 nanometers (nm), for most oxide layers as grown from a substrate like silicon (Si) interlayer thickness determination as a general admitted concept, is to consider a fixed value of the refractive index (r.i.), e. g. either 1.457 1.46 at 633nm or less considering native oxide ( currently most native oxide are 1.0 to 2.5 nanometer-thick). Initial first theories were most involving this“ as transition layer” describing the fact that in nature no discontinuities exist. With native oxide the classical models use often a parametrized Cauchy or Sell Meyer law as shown here, i. e.
(1) 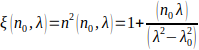
or an equivalent “ absorption Urbach tail edged” formula associated with
(1-a) ![]()
with λ as the light wavelength, the validity remains inside a specified interval range( e. g. the Urbach absorption tail in edge of the visible range). For example, we have n633nm =1.99 and nslope =0.03 for zinc oxide (ZnO).[8] These parameters are well-known for years from thicker samples works. Yet in the nineteens, these models were refined introducing also a more or less densified materials concept through the Effective Medium Approximation (EMA). The Lorentz Lorenz equation for a mixture of material whose complex dielectric constants and volume fractions are respectively and fi and the Bruggeman formula for computingin terms of and fi is, The are respective relative volume fractions for host and depolarizing electric field with spherical voids and the film optical index with The thickness tF . For calibrated samples with electron microscopy can then be used as references too.
1.a The Instrumentation Developments
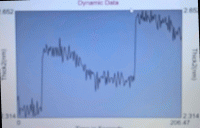
Among SE candidates choosing the SE instruments “single shot SE “ are very attractive. As a new instrument generation, they affords direct real time observation access of the phenomena within short time scale less than 50 milliseconds (ms). Considering analytical models, not only one but with a limited number of wavelengths is also a sufficient criterium. Single shot SE are thus really to be chosen. Today as a pioneer and prior than these future instruments has been afforded, exist the commercially available fast Wide Band multi-Wavelength Ellipsometers already seen as “no moving part “ [9] But it is not unique. In these last years, new systems should be soon reported in literature. See the last R. A. Azzam retrospective [10]. These future designs can be denominated also by “single shot ellipsometer” or “no moving parts” Ellipsometer or polarimeters. They are the near future tools in real time dynamic processing. They are also accurate when their limit reaches the quantum noise “glass ceiling” seen as the intrinsic source “photon noise limit”[11-a]. Only new quantum dots pulse light sources might overcome it. Presently, let us show and comfort the ability to drive any thin layer material growth. This important aspect indeed goes with the scaling down below 5 nm-thickness as it is presently for the nano 3-D scale domain of the IC technologies. Spectroscopic Ellipsometry, (SE) must provide also a plain real time fast enough quality control tool. If spectroscopic measurements requires the largest possible spectral range for new materials, the bill to pay is an increase of the acquisition time during measurements. In industry, there are no needs to measure so many usefulness wavelengths data. The analytical models describing most dielectrics in the visible range exist and are known since the nineteens and present database available on the web [12]. The use some how of a first candidate under this “one single shot ellipsometer” termination is thus of concern. A multi wavelengths division-of-amplitude ellipsometer (DOA) is an old concept from the first papers of R. Azzam , G. Tompkins , E. A. Irene[13 ]. Together with providing an additional parameter, the degree of polarization P is a not yet well interpreted. The no “moving parts” aspect and ”new” LED sources use, prevents from tedious alignments and limited life time sources replacements procedures. Furthermore LEDs sources own less noise than the classical Xe xenon sources of the first instruments [10]. Each acquisition step displays in real time the N, C, S classical stoke vector components values. A full description can be found from supplier’s white papers and implicit patents[14]. With a limited number of 4 wavelengths, this concept yields a fast acquisition mode without any moving optical elements in the beam with a roughly 50-100ms acquisition rate, covering the visible range with these wide LEDS bands at respectively 463, 524, 595 and 637nm wavelengths. This wavelengths number is not unique as it is now 6 in the latest instrument versions. It also runs at a very fast acquisition modes. Spectral range cover efficiently the visible range. This SE can be seen as a first pioneer tool with up to six wavelengths available today. Nevertheless one has to keep in mind that other solutions using new integrated photonic designs exist and a wish is to see them soon available in commercial versions. As other perspectives, an additional parameter which will be review later in this paper is a value of the degree of polarization Pexp which should be equal to the degree of polarizationand introduces a surface roughness parameter due to light diffusion as we shall see hereafter. Some slight modifications of the instrument could turn even them into a complete polarimeter as well. An other advantage is that no tedious alignments are involved before the ellipsometry ratio can be retrieved. The quantities related to the reflected Stoke vectors of light by the surface are measured. Dynamic data for real time process directly provides the equivalent normalized Stokes vector S= {-S1/S0, S2/S0, -S3/S0} usually represented on the Poincaré sphere of radius |S|=1. Single, continuous and dynamic measurements turn today to be in the basic software tools. An additional advantage is the remote access. Extracted from a measurement area through VNC (Virtual Network Communication) software become a high advantage when internal internet connected objects (IoT) are concerned as seen also here later. To a short overview from data acquisition, one obtains the well known ellipsometry usual angular values Ψ, Δ , P associated to ρ=C+j S/(1+N) with N=cos 2Ψ , C=sin2Ψ cos Δ and S= sin2 Ψ sin Δ The streaming mode stores directly data and fasten acquisition rate. Data are being later re-analyzed or parallely processed. Both incidence angle aoi= and substrate refractive index nsubstrate (or n2 ) values affect only ρo the origin ordinate and ρo refer ideally only to a bare surface (tfilm=0). The accuracy limit could be also originated from the angle of incidence (aoi) selecting various position shifts of the samples in the xy mapping experiment. Here the refractive index remains of the order of a 10-2 accuracy range. It’s definitely better the case for in situ systems with a fixed previous alignment and no modulating elements.